Wie man Passwörter knackt
Fast jede App und jeder Online-Dienst verlangt das wir uns registrieren. Und jedes mal sollen wir ein sicheres Passwort wählen. Nur: Wann ist ein Passwort sicher? Um besser zu verstehen, welche Passwörter gut sind und welche nicht, schauen wir uns einmal an, wie Passwörter geknackt werden.
Weil Passwortsicherheit eigentlich eine sehr mathematisch, theoretische Angelegenheit ist, wollen wir uns das Ganze an einer kleinen Geschichte verdeutlichen.
Unsere fiktive Heldin Eva Evil ist Software-Entwicklerin und hatte genug von schlecht bezahlten Startup-Jobs. Zusammen mit ihrem Kumpel Malroy Malice hat sie sich selbstständig gemacht. Ihre gemeinsame Firma “E&M Labs” hat sich auf die Verbreitung von Spam und Malware spezialisiert. Und weil man das von überall machen kann, liegt ihr Büro auf einer Karibikinsel mit laxen Gesetzen aber schönen Stränden. 🏝
Online-Angriffe
Über einen anonymen Online-Marktplatz für Hacker hat E&M heute morgen einen einfachen aber gut-bezahlten Auftrag erhalten. Eva soll sich Zugang zum E-Mail-Konto eines deutschen Geschäftsmannes verschaffen und dort nach kompromittierenden Bildern für eine Erpressung suchen.
Dazu muss sie sein Passwort erraten. Anders als in Filmen, macht sie das nicht von Hand sondern hat ein Programm, das für sie die Passwörter automatisch durchtestet. Normalerweise kann man bei Online-Konten nur eine begrenzte Zahl von Passwörtern ausprobieren, bis der Dienst die Login-Versuche künstlich verlangsamt. Zum Glück hat gerade dieser Dienst eine fehlerhafte Schnittstelle, über die man uneingeschränkt viele Login-Versuche machen kann. So ist die Zahl der Login-Versuche, die Eva pro Sekunde machen kann nur durch ihre Internet-Geschwindigkeit limitiert und sie schafft pro Sekunde über 100.
Aus dem Internet hat Eva eine Liste mit den 10.000 häufigsten Passwörtern runtergeladen. Alle zu prüfen dauert so nur etwa 100 Sekunden. Und tatsächlich hat das Programm nach knapp einer Minute das richtige Passwort gefunden: james007. Nach fünf weiteren Minuten hat Eva alle E-Mails runtergeladen.
Auftrag erledigt. Zeit für einen Kaffee. 🥐☕️
Offline Angriffe
Evas Ziel für den Nachmittag ist etwas kniffeliger, aber sie will heute früh Schluss machen und noch ein paar Cocktails am Strand trinken.
Das Hauptgeschäft von Evas Firma ist Spam, den Sie im Auftrag von Pillenfälschern, Pornoseiten und Malwareherstellern verschicken. Als Premium-Dienst bieten Eva und Ihre Kollegen an, Spam von gehackten privaten E-Mail-Konten an die jeweiligen Freunde des Konto-Inhabers zu verschicken. Solche Spam-Mails sind kaum von echten zu unterscheiden und sind ideal um beispielsweise Malware zu verteilen.
Nur, wie kann Eva tausende E-Mail-Konten an einem Nachmittag hacken? Ihr Kollege Malroy hat ihr heute Morgen eine Liste von 1 Million Zugangsdaten von Nutzern der fiktiven Fitness-App “Suffr” gegeben. Die konnte er dort gestern entwenden, weil die Server nicht richtig gesichert waren.
Dass solche Listen mit verschlüsselten Passwörtern verloren gehen, passiert (zum Glück für Eva und ihre Kollegen) sehr viel häufiger als man denkt.
| Passwort-Hash | |
|---|---|
| aaron@appleseed.com | 1f3870be274f6c49b3e31a |
| alice93@banana.com | 72b302bf297a228a757301 |
| annemarie_x@jmail.com | c4ca4238a0b923820dcc50 |
| anton.hip@banana.com | 912ec803b2ce49e4a54106 |
| august@us.net | 5a60668bacacd99584dcc0 |
| … | … |
| zaccharias@last.com | a77224c90dc6867f603a3a |
Jeder Eintrag besteht aus der E-Mail-Adresse des jeweiligen Nutzers und dem dazugehörigen verschlüsselten Passwort. Online Dienste speichern Passwörter (zum Glück) fast immer verschlüsselt mit sogenannten Hash-Funktionen. Das sind mathematische Funktionen, die eine Eingabe (das Passwort) in ein verschlüsseltes Format, den sogenannten Hash, umwandeln.
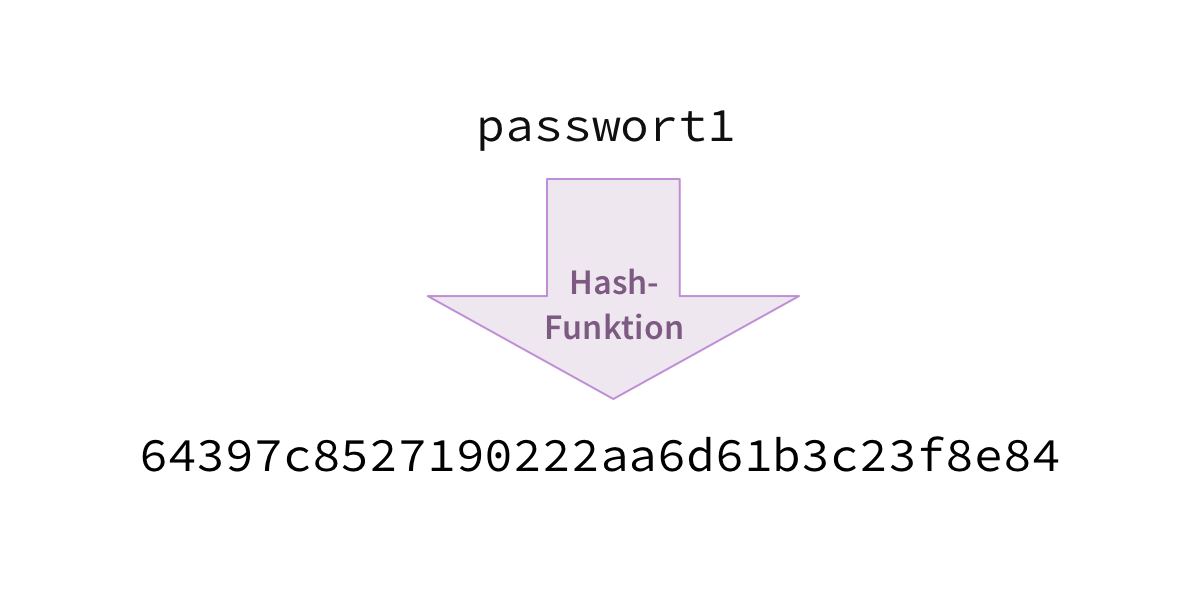
Eine Hash-Funktion unterscheidet sich von einer üblichen Verschlüsselung darin, dass die Funktion unumkehrbar ist. Eine normale Verschlüsselung kann man — wenn man das Passwort kennt — einfach wieder umkehren und so den Originalinhalt lesen.
Von einem Hash lässt sich jedoch grundsätzlich nicht auf die Originaleingabe schliessen. Daher ist für das Hashen auch kein Passwort nötig.
Wenn du dich an deinem Computer oder irgendeinem Online-Konto mit deinem Passwort anmeldest, wird aus deinem Passwort der Hash-Wert berechnet und mit dem für deinen Benutzernamen gespeicherten Hash verglichen. Wenn beide gleich sind, erhältst du Zugang.
Die einzige Möglichkeit das Originalpasswort zu finden ist, selbst solange verschiedene Passwörter mit der gleichen Hash-Funktion zu verschlüsseln bis eines einen identischen Hash ergibt. Das “Passwort-Knacken” besteht also auch hier einfach im simplen Ausprobieren, wie bei einem Zahlenschloss.
Eva kann jetzt lokal auf ihrem Computer die Passwörter testen. Für solche Aufgaben haben Eva und Malroy einen kleinen Server-Raum mit 5 Rechner mit jeweils mit 5 Graphikkarten, die zusammengeschlossen sind. Damit schaffen sie es pro Sekunde unvorstellbare 350 Milliarden Passwörter zu testen.1
Passwort-Listen
Eva fängt an mit einer Liste von 300 Millionen Passwörtern aus schon früher gestohlenen Passwort-Datenbanken. Das sind also alles Passwörter, die zuvor schon mal irgendjemand irgendwo verwendet hat. Es ist sehr wahrscheindlich, dass viele Nutzer von Suffr entweder das selbe Passwort verwenden, das sie schon mal bei einem der gehackten Dienste benutzt haben oder, dass sie zufällig das selbe Passwort wie jemand anders benutzen, weil ihr Passwort nicht so einzigartig ist, wie sie dachten. Die häufigsten Passwörter sind tatsächlich so trivial wie hallo, passwort oder 123456.2
Für jedes verschlüsselte Passwort testet sie nun also die 300 Millionen Passwörter durch. Mit ihrem kleinen Superrechner kann Sie so pro Sekunde somit 1000 Konten testen. Nach etwas weniger als 20 Minuten ist sie durch und konnte so 70% der Passwörter finden.
Regel-Basierte Angriffe
Weil sie noch etwas Zeit hat, bevor die Happy-Hour in der Strandbar anfängt, will sie jetzt noch einen sogenannten Wörterbuchangriff auf die restlichen 300.000 Passwörter durchführen. Viele Nutzer verwenden als Passwort ein Wort und hängen zur Sicherheit noch eine Zahl und/oder ein Sonderzeichen an. Das ergibt Passwörter wie Schnucki1!, unknackbar!! oder Teddibär68.
Also Nimmt Eva je eine Liste aller Englischen und aller Deutschen Wörter. Das sind insgesamt knapp 400.000 Wörter. Eva gibt ihrem Hacking-Programm noch die Regel vor, die Wörter sowohl mit dem ersten Buchstaben gross und klein zu testen und dann noch jeweils alle Kombinationen von 0–2 Zahlen und/oder Sonderzeichen anzuhängen. Das ergibt insgesamt 1,3 Milliarden Passwortkombinationen. 3
Mit ihrem Graphikkarten-Cluster kann Eva ein einer Sekunde für 270 Konten alle diese 1,3 Mrd Kombinationen testen und schafft so in weniger als 20 Minuten alle verbliebenen 300.000 Konten durchzugehen. Dabei kann sie tatsächlich nochmal 100.000 Passwörter knacken.
Jetzt hat sie in knapp einer Stunde 800.000 E-Mail und Passwort-Kombinationen gefunden. Bei sehr vielen von den betroffenen NutzerInnen wird das geknackte Suffr-Passwort das selbe sein, das sie auch für ihr E-Mail-Konto benutzen. Diese E-Mail-Konten wird ihr Kollege Malroy dann morgen übernehmen und die erste Welle aus Spam-Mails über sie verschicken. ✉️
Brute-Force Angriffe
Bevor Sie geht startet Eva schliesslich noch einen sogenannten Brute-Force-Angriff. Dabei werden einfach alle möglichen Kombinationen aus einem bestimmten Zeichensatz durchprobiert. Bei je 26 Gross- und Kleinbuchstaben plus Zahlen und Sonderzeichen gibt es 95 Zeichen, die in der Regel für ein Passwort in Frage kommen. Für ein Passwort mit 6 Zeichen gibt es also insgesamt 956 mögliche Kombinationen. Das sind ca. 735 Milliarden. Die könnte Eva für ein verschlüsseltes Passwort mit ihrem Superrechner in 2 Sekunden alle durchgehen. Da Suffr aber als Mindestlänge 8 Zeichen vorgegeben hat, ist es nicht ganz so einfach. Mit der Länge wächst die Zahl der möglichen Zeichenkombinationen nämlich exponentiell und 958 ergibt bereits über 6 Billiarden mögliche Kombinationen. Eva würde mit Ihrer Hardware hier schon über 5 Stunden für ein einziges Passwort benötigen. Wenn sie es nur auf einen bestimmten Nutzer abgesehen hätte, wäre das kein Problem. Aber sie hat ja noch 200.000 verschlüsselte Passwörter.
Aber auch hier lässt sich die Zeit deutlich reduzieren, wenn man nicht alle Kombinationen testet, sondern nur solche, die die meisten Menschen wählen würden. Eva geht davon aus, dass die Passwortregel von Suffr, dass ein Passwort einen Grossbuchstaben, ein Sonderzeichen und eine Zahl enthalten muss, dazu führt, dass die meisten Leute nur einen Buchstaben gross schreiben und ans Ende eine Zahl und ein Sonderzeichen hinzugefügt haben. Ausserdem will sie nur die Passwörter testen, die genau acht Zeichen haben, weil wohl nur wenige NutzerInnen sich die Mühe gemacht haben ein längeres Passwort zu wählen. Das sind dann eigentlich sehr zufällige Passwörter wie Ohmjkn8$, fjZcwk?3 oder srqfyR#0. Insgesamt gibt es ca. 740 Milliarden Passwörter nach diesem Muster.4 Um alle durchzugehen braucht Eva also knapp 2,1 Sekunden. Um das für alle verbliebenen 200.000 Passwörter zu machen braucht sie damit etwas weniger als 5 Tage. Sie beschliesst die Rechner einfach über das lange Wochenende laufen zu lassen.
Am nächsten Dienstag hat sie noch einmal 50.000 Passwörter geknackt. 🍹
Die Moral der Geschichte
Evas und Malroys Hacker-Business und die technischen Beispiele sind natürlich stark vereinfacht und im echten Leben etwas nuancierter.5
Trotzdem können wir daran gut sehen, welche Faktoren für ein gutes Passwort wichtig sind.
- Passwörter, die aus einem normalen Wort, Namen oder Ort bestehen, sind in Millisekunden geknackt.
- Einfach eine Zahl und/oder ein Sonderzeichen an ein Wort zu hängen, reicht nicht um es sicher zu machen.
- Jedes Passwort, das schon mal jemand anderes irgendwo auf der Welt benutzt hat oder benutzen könnte, ist unsicher. Jeder Hacker wird zuerst diese bekannten Passwortlisten durchtesten.
- Hacker können oft unvorstellbar viele Passwörter in sehr kurzer Zeit testen. Der Supercomputer, den Eva benutzt, ist nicht erfunden, sondern wurde bereits 2012 so von Wissenschaftlern gebaut.1 Er ist nichtmal besonders teuer. Eine gute Graphikkarte kostet etwa €500. Mit 25 davon kostet der Rechnerverbund vielleicht €15.000. Wir müssen also jetzt — 7 Jahre später — davon ausgehen, dass der durchschnittliche Hacker durchaus 1 Billion Passörter pro Sekunde testen kann.
- Am schwierigsten sind für Eva die Passwörter, die sie per Brute-Force knacken muss. Das sind in der Regel Zufalls-Zeichenketten. Und je länger diese sind, desto schwieriger sind sie zu knacken.
Wenn du deine Passwörter wirklich sicher gestallten willst, solltest du einen Passwort-Manager (z.B. 1Password) verwenden und dir von diesem für jeden Online-Dienst ein langes Zufalls-Passwort erzeugen lassen.
Und weil der Passwort-Manager diese bequem für dich speichert, musst du sie dir auch nicht merken.
Update: Im Artikel “Sichere Passwörter wählen” bekommst du Tipps, wie du dir ein merkbares aber sicheres Passwort erzeugst.
-
ArsTechnica Artikel vom 25. Dezember 2012: “25-GPU cluster cracks every standard Windows password in <6 hours” ↩︎
-
Liste der 25 häufigsten Passwörter in Deutschland ermittelt vom Hasso-Plattner-Institut ↩︎
-
Es gibt 10 Ziffern und 30 Sonderzeichen. Bei 1–2 Stellen ergeben sich 40 + 402 = 1640 Kombinationen. Wenn man das mit den 800.000 (Grosser und kleiner Anfangsbuchstabe) Wörtern kombiniert (multipliziert) sind es insgesamt knapp 1,3 Milliarden Passwortkombinationen. ↩︎
-
Unsere Regel sieht vor, dass die ersten 6 Zeichen aus 5 Kleinbuchstaben und 1 Grossbuchstaben bestehen. Dafür gibt es 266 · 6 ≈ 1,8 Milliarden Möglichkeiten. Für die letzten beiden Zeichen aus Ziffer und den 20 häufigsten Sonderzeichen gibt es 10 · 20 · 2 = 400 Kombinationen. ↩︎
-
Ars Technica hat 2013 für einen ausführlichen Artikel über das Passwort-Knacken einmal drei echten Sicherheitsexperten beim Knacken einer Passwort-Liste über die Schulter geschaut ↩︎